とある京大生のホームページのTOP >
数学全般 >
ド・モアブルの定理
ド・モアブルの定理
すいません・・・しばらくサボっていたので、久々の更新になります。
今日は、ド・モアブルの定理を紹介したいと思います。有名なので知っている方も多いかとは思いますが・・・
◎ ド・モアブルの定理
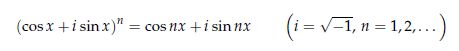
この定理の左辺のn乗を展開して実部・虚部を比較することで、三角関数のn倍角の公式を導くことができます。
[証明]
証明はPDF版のこちらをどうぞ。
| とある京大生のホームページ |
|
とある京大生のホームページのTOP >
数学全般 >
ド・モアブルの定理
ド・モアブルの定理 すいません・・・しばらくサボっていたので、久々の更新になります。 ◎ ド・モアブルの定理 この定理の左辺のn乗を展開して実部・虚部を比較することで、三角関数のn倍角の公式を導くことができます。 [証明] |
カテゴリー月別アーカイブリンク |
| Copyright © 2008 by Toaru-High School Student |
こんにちは。「n倍角の公式」に反応しました。
CEGIPOと申します。一応社会人です。
(すみません。勝手にお邪魔します。(^_^;))
三角関数の cosθ,sinθ,tanθのn倍角の公式は、
ド・モアブルの公式をうまく利用するとスマートに
表せますよね。展開する前の一般式について
ちょっと工夫して考えてみました。
[ド・モアブルの定理]
a^bをaのb乗、
θを任意の実数、nを任意の自然数,iを虚数単位として、
(cosθ+isinθ)^n=cos(nθ)+isin(nθ) ...(式1-1)
このθを-θに置き換えて書いてみます。
(cos(-θ)+isin(-θ))^n=cos(n・(-θ))+isin(n・(-θ))
(cos(-θ)+isin(-θ))^n=cos(-nθ)+isin(-nθ)
cos(-θ)=cosθ,cos(-nθ)=cos(nθ),
sin(-θ)=-sinθ,sin(-nθ)=-sin(nθ)
だから、
(cosθ-isinθ)^n=cos(nθ)-isin(nθ) ... (式1-2)
(式1-1),(式1-2)の両辺の和と差をとって、
{(cosθ+isinθ)^n+(cosθ-isinθ)^n}=2cos(nθ)
{(cosθ+isinθ)^n-(cosθ-isinθ)^n}=2isin(nθ)
整理して、
cos(nθ)= {(cosθ+isinθ)^n+(cosθ-isinθ)^n}/2
...[cosのn倍角の公式]
sin(nθ)=-i{(cosθ+isinθ)^n-(cosθ-isinθ)^n}/2
...[sinのn倍角の公式]
が得られます。
さらに、cosθ≠0の時は、
tan(nθ)
=-i{(cosθ+isinθ)^n-(cosθ-isinθ)^n}
/{(cosθ+isinθ)^n+(cosθ-isinθ)^n}
=-i{(1+itanθ)^n-(1-itanθ)^n}
/{(1+itanθ)^n+(1-itanθ)^n}
すなわち、
tan(nθ)
=-i{(1+itanθ)^n-(1-itanθ)^n}
/{(1+itanθ)^n+(1-itanθ)^n}
...[tanのn倍角の公式]
が得られます。
___
三角関数のn倍角の公式は、
フィボナッチ数列の一般項の式の構造によく似ています。
(フィボナッチ数列では、値が自然数なのに、
一般項式は√を含む。
n倍角の公式では、値が実数なのに、
一般項式は複素数を含む。
(なぜかなぁ?何か理由があるのかも知れないですね。)
投稿者: CEGIPO | 2008年6月20日 20:06
>> CEGIPO さん
コメントありがとうございます。
三角関数のn倍角の公式については、求め方を丁寧に書いてくださりとても分かりやすかったです(tanまで求めてくださるとは・・・)。
ですが最後の質問については、正直なところ僕には難解な内容です。
フィボナッチ数列の一般項は
(1/√5)・[{(1+√5)/2}^n-{(1-√5)/2}^n]
でしたよね。確かにn倍角の公式に似ていますし、√5が出てくるのも不思議です。何か理由でもあるのでしょうか・・・。
本やらを引っくり返して色々調べてみましたが、今のところ手がかりになりそうなものは見つかっていません。
数の範囲を拡張(自然数から実数、実数から複素数)しないと求められないというところがポイントなのでしょうか?
いずれにせよ、まだ考えたりする余地がありそうなので、もう少しトライしてみたいと思います。
投稿者: とある高校生 | 2008年6月22日 12:57
n≦0の場合に、ドモアブルの定理が成り立つことって証明できますか?
投稿者: のの | 2010年4月21日 22:37
コメントありがとうございます。
数学的帰納法ではn>0の場合のみですが、n≦0 の場合でも証明できます。
・n<0 のときは、n=-m (m>0)とおいてあげて、オイラーの公式から式変形することで証明することができます。式変形は
http://www.sumita-planning.jp/~shunta/blog/images/20100422/formula1.jpg
をご覧ください。
・n=0 のときは、一般性を失わないために0乗を1と"定義"することになります。"証明"ではありませんが。
http://www.sumita-planning.jp/~shunta/blog/images/20100422/formula2.jpg
投稿者: とある高校生 | 2010年4月22日 18:56